Digital Option Market Making on Prediction Markets
I was supposed to write on fast message parsing using simd intrinsics and orderbook implementation, but I am abit too swamped at the moment. I picked a topic that is abit shorter and seems to be on the cusp of many’s interests.
Betting markets are all the rage. Of a particular kind are event contracts that are just digital options. They are on Kalshi. Our prediction market arb lectures take a slightly different approach;
but we will stick to digital options for today. Today’s post is brought to you by Autonity:
🧠 Forecastathon Season 2 – Where Models Meet Markets
The Forecastathon is a global competition where traders, builders, and forecasters test their skills on real-world data using a new class of derivatives called Forecast Futures: contracts that track market expectations of future outcomes and settle directly on verified results such as CPI, GDP, Climate metrics etc.
👉 Join Season 2: http://shorturl.at/F0QIG
Unlike binary prediction markets, Forecast Futures offer linear payoffs, rewarding both forecasting precision and risk management. Season 1 demonstrated how the Autonity community coordinated forecasting and trading around macro indicators like CPI and jobless claims, powered by the Autonomous Futures Protocol (AFP) and cleared fully on-chain. Teams played an active role in shaping strategies, showing how collaboration enhances collective performance and deepens participation. Participants can join or form teams until Oct 27 (15:00 GMT) or compete solo. Team members unlock additional rewards from a 165,000 NTN pool across all three seasons.
👥 Create/Join Teams: http://shorturl.at/7bLm4
Season 2 builds on that foundation with new crypto, weather, and macro underlyings, introducing more sophisticated contract types designed for dynamic real-world data. The Forecastathon scoring spans four categories: portfolio performance, forecasting accuracy, market making, and product creation within a total 300,000 NTN prize pool. Explore how data, markets, and collective intelligence converge on the first blockchain built for autonomous futures. If you’d like to learn more about the Forecastathon, read:
📘 Why Does the Forecastathon Matter?
📗 The Forecastathon: Where Models Meet Markets
🫱 Join Season 2: https://shorturl.at/F0QIG
👫 Create/Join Teams - https://shorturl.at/7bLm4
📈 Start Forecasting: http://forecastathon.ai/forecasting
💹 Trade Live Markets: http://autex.exchange
👨💻 Build with the AFP SDK: http://github.com/autonity/afp-sdk
🤖 Explore AFP Agents: http://github.com/autonity/afp-agents
Now, into the stuff.
Digital Options/Binary Options
They go by different names but are the same beast. The payoff structure is simple, and hence so is their pricing (theoretically).
We will cover a cash-or-nothing binary call that pays $1 if the underlying stock price S_T exceeds the strike (K) at expiration (T), and $0 otherwise (ignoring pin risk at exactly (K)). We’ll use a notation where time is (y) (current time), stock price is S_y and τ = = T - y is the time to expiration. The fair price is denoted F_y.
Unlike vanilla options, which have a linear payoff beyond the strike, digitals pay a fixed amount (e.g., $1) if a specific condition is met at expiration. They are popular in betting markets, because well, isn’t it fun? If you like coin flipping, you will love this. But you should stick to coin flipping, I think.
From a market-making perspective, delta hedging is challenging, especially given how near-expiry these tend to be and the jumps in high frequency data. The result is that the bid-ask gets incredibly wide for near-expiry contracts. It’s like 0DTE but worse. On the plus side, you have a capped inventory loss since the loss is -1 or 0 instead of -max(S_T - K,0).
But if you were so interested as to read this post, I assume you are interested in these markets. You should at least be equipped with knowledge to be stated…
Fair Price Formula
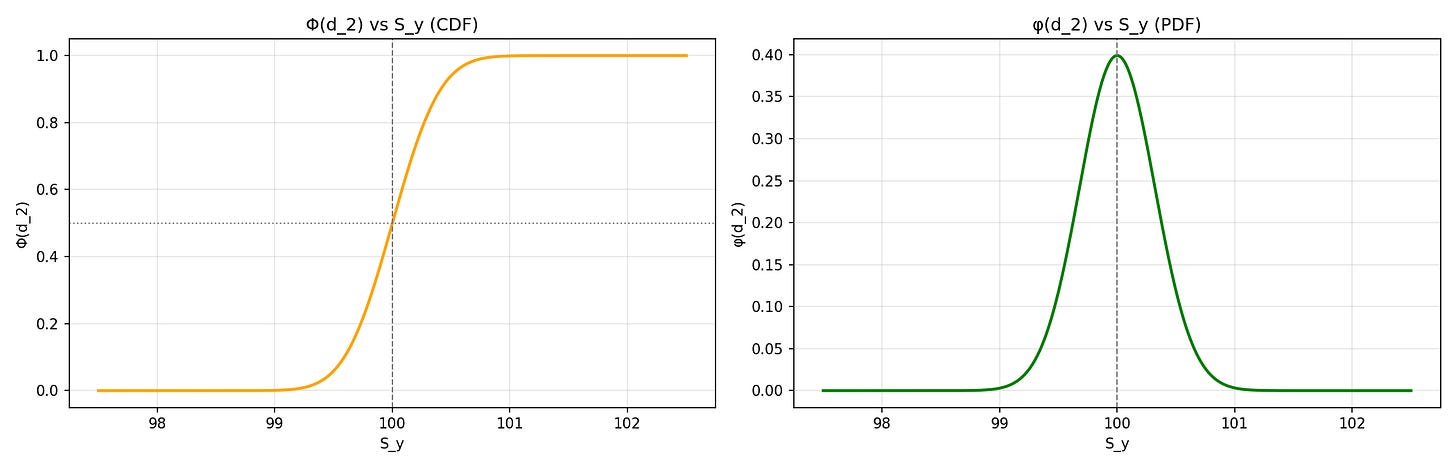
Fair price of a digital option under the Black-Scholes model is derived from the risk-neutral probability that the option finishes in-the-money.
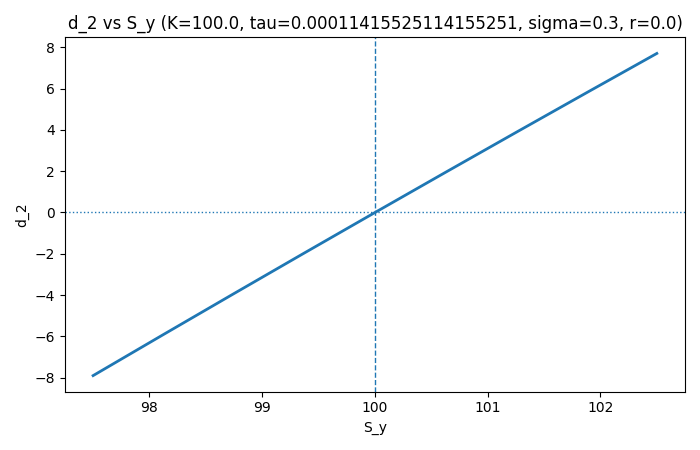
where Phi is CDF standard normal and d_2 is
the standard risk-free in crypto could just be the default borrow (popular value 0.0013%/H) for perp funding. Or, for short tenors we can treat r = 0 and get rid of the second term. Accordingly, we also get rid of the discount factor. This is your theoretical mid. Everything is known except for σ.
For a quick mental reference, I picked tau = 1 * 1/365 * 1/24 (1 hour) - d_2 is looks linear ATM because ln(1 + x) ~ x, remember? It is the log-moneyness that is exactly linear.
Spread
Before we go into finding vol, a reasonable theoretical spread should be the cost-of-hedging. This is scaled relative to
These are actually terms that appear in the Greeks of the fair price. Rather than go into the math, it is simple to intuit - each term is the uncertainty w.r.t the price changes. Vol speaks for itself. Sqrt of expiry is the amount of time volatility has left to act. The density function takes the shape of the Gamma curve and encodes how “in-the-money” or “out-of-money” it is.
In practice, this is determined by more factors, your hedging cost, vol calibration errors, inventory and adverse fill costs. The calibration to vol is a matter of choice;