Feature resampling and Simulating on Tick Data for Trading (w code)

Now that market volatility and alt prices are back in fashion, cross exchange and funding arbitrageurs are back in style. We released our funding arbitrage lectures, streaming 12.5 hours on the theory and design in implementation of a fully-systematic multi-exchange/asset perp arbitrage setup in Python:

https://lectures.hangukquant.com/courses/qt410

(400 USD off for 1 week)

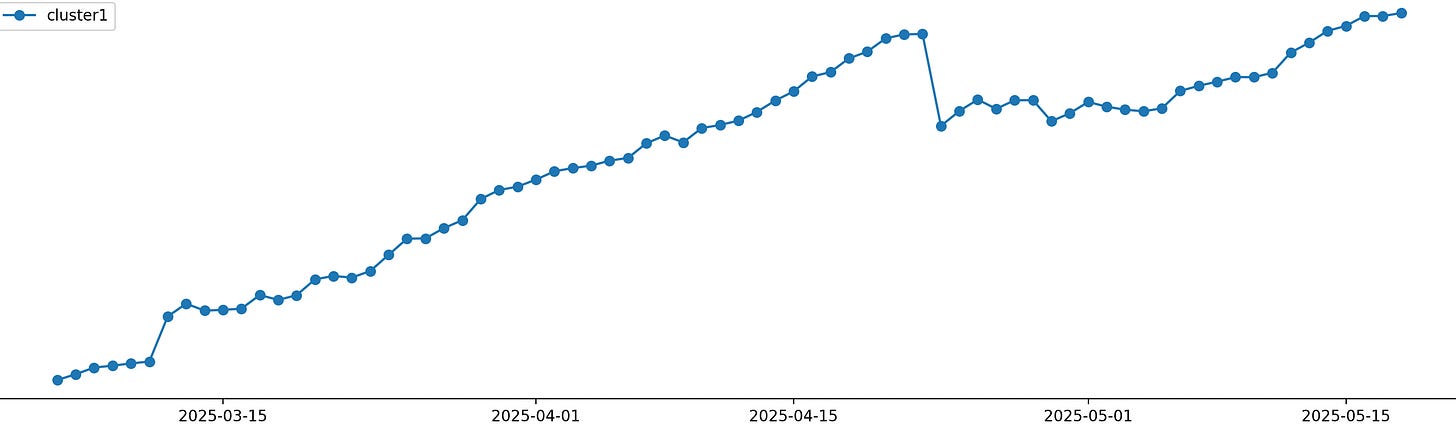
Here is my own live pnl:

And…before we get into the post, I wanted to give a shout out to my recently created quant lecture series, which I have placed a max-discount on Udemy for 5 days.

In the previous post, we talked about sampling information bars. This post goes in greater detail; shows code and some numerical trials using live tick data.

Feature Resampling

Feature resampling, in the context of machine learning, is a technique used to address class imbalance in datasets. It involves modifying the dataset by either increasing the number of instances in the minority class (oversampling) or reducing the number of instances in the majority class (undersampling).

Tick data feeds are often aggregated into candlestick bars. Classical candlesticks are sampled with respect to time, but this choice is fairly arbitrary — for one, we know that markets do not trade at a uniform speed (Kyle & Obizhaeva, de Prado). For instance, market open and closing hours tend to be more liquid.

Time bars oversample information during periods of low activity, and vice versa. Consequently, time sampling often exhibit poor statistical properties.

Sampling as a function of other variables, such as number of transactions (Mandelbrot, 1963), allows us to achieve samples closer to i.i.d. Gaussian distributions, making them more amenable to statistical modeling and interpretation.

Typical information included in aggregated bars include

• t (start),

• open, high, low, close, volume,

• n (number of ticks),

• vwap,

• T (end).

Time bars, tick bars, volume bars, dollar bars, signed tick/volume/dollar bars are defined as follows:

Probabilistic Bars

The above bars are somewhat static, but we would like to perform sampling with frequency proportional to the arrival of information. This new paradigm of information sampling works on a dynamic frequency with respect to deviation from some expected thresholds; we define probabilistic bars as follows:

Small Numerical Trial

A small numerical test is proposed to observe if BTC trade ticks exhibit mean-reversionary effects to vwap levels. Volume is often considered to be a metric of informed traders with asymmetric information crossing the bid-ask spread. It is reasonable to suspect that prices with higher volumes act as anchors. We test this relation using a simple regression relationship between time-series bar samples:

The trials are repeated for (i) classical time bars, and (ii) probabilistic bars.

Using quantpylib's features and Binance websocket data,

i) data is first archived.

ii) archived data is restored and passed through the mock data replayer to simulate real time feed at null latency.

iii) custom bar feeds are subscribed through the feed object using the tick feed with hft.bars logic.

See tick data management tutorial here. Documentation is here for the hft module.

The code for regression trials and subscribing to the custom bar feeds is presented at the bottom.

The sampled bars are retrieved as in bar_feed.as_df():

We obtained the following results for time-based sampling (not significant) and probabilisitic sampling (significant):

Clearly, the numerical experiments reveal some interesting dynamics between sampling behaviour and the presence of mean-reversion effects. Not as clearly, it is important to keep in mind these are time-varying effects, and most perhaps regime dependent.

import pytz
import json
import asyncio  
import matplotlib.pyplot as plt

from datetime import datetime
from dateutil.relativedelta import relativedelta

import quantpylib.hft.bars as bars
from quantpylib.hft.feed import Feed
from quantpylib.gateway.master import Gateway 

show = False
exc = 'binance'
tickers = ['BTCUSDT']
stream_data = {
    'binance': tickers,
}

run = None
time = None
replayer = None

from quantpylib.hft.mocks import Replayer,Latencies

hours = 10
now = datetime.now(pytz.utc)
start = now - relativedelta(hours=hours)
start = start.strftime('%Y-%m-%d:%H')
end = now.strftime('%Y-%m-%d:%H')

LATENCY = 0
latencies={
    Latencies.REQ_PUBLIC:LATENCY,
    Latencies.REQ_PRIVATE:LATENCY,
    Latencies.ACK_PUBLIC:LATENCY,
    Latencies.ACK_PRIVATE:LATENCY,
    Latencies.FEED_PUBLIC:LATENCY,
    Latencies.FEED_PRIVATE:LATENCY,
}
replayer_configs = {
    "latencies":latencies,
}

gateway = Gateway(config_keys={"binance": {}})

async def handler(bar):
    print(bar)

async def play_data(replayer,oms,feed,ticker):
    trade_feed_id = await feed.add_trades_feed(
        exc='binance',
        ticker='BTCUSDT',
        buffer=100,
    )
    time_bars = await feed.add_sampling_bars_feed(
        exc='binance',
        ticker='BTCUSDT',
        handler=handler,
        buffer=10000,
        bar_cls=bars.TimeBars,
        granularity='m',
        granularity_multiplier=3,
    )

    probabilistic_bars = await feed.add_sampling_bars_feed(
        exc='binance',
        ticker='BTCUSDT',
        handler=handler,
        buffer=10000,
        bar_cls=bars.ProbabilisticSignedTickBars,
        n_ticks=1500,
    )
    return time_bars,probabilistic_bars

async def hft(replayer,oms,feed):
    bar_feeds = await asyncio.gather(*[
        play_data(replayer=replayer,oms=oms,feed=feed,ticker=ticker) 
        for ticker in tickers
    ])
    await run()
    for _type,_bar_feed in zip(['time','probabilistic'],bar_feeds[0]):
        bar_feed = feed.get_feed(_bar_feed)
        bars = bar_feed.as_df()

        from quantpylib.simulator.models import GeneticRegression
        configs = {"df":bars}

        model = GeneticRegression(
            formula="div(forward_1(c),c) ~ div(minus(c,vwap),c)",
            df=bars
        )
        res = model.ols()
        model.plot()
        print(res.summary())

async def sim_prepare():
    trade_data = {exchange:{} for exchange in stream_data}

    for exchange,tickers in stream_data.items():
        trade_archives = [
            Feed.load_trade_archives(
                exc=exchange,
                ticker=ticker,
                start=start,
                end=end
            ) for ticker in tickers
        ]

        trade_data[exchange] = {
            ticker:trade_archive 
            for ticker,trade_archive in zip(tickers,trade_archives)
        }

    global replayer, run, time
    replayer = Replayer(
        l2_data={},
        trade_data=trade_data,
        gateway=gateway,
        **replayer_configs
    )
    oms = replayer.get_oms()
    feed = replayer.get_feed()
    run = lambda : replayer.play()
    time = lambda : replayer.time()
    return oms, feed

async def main():
    await gateway.init_clients() 
    oms,feed = await sim_prepare()    
    await oms.init()
    await hft(replayer,oms,feed)
    await gateway.cleanup_clients()

if __name__ == '__main__':
    asyncio.run(main())