Formulaic Alpha Report - Insight on Signal Migration and the Fundamental Law of Active Management

Preview:

In the previous week, we discussed the Feynmac Kac theorems and their relation to continuous time asset pricing. In the next week, we continue the discussion on asset pricing and use the techniques discussed to introducing formalisms for risk premiums and risk-neutral asset pricing.

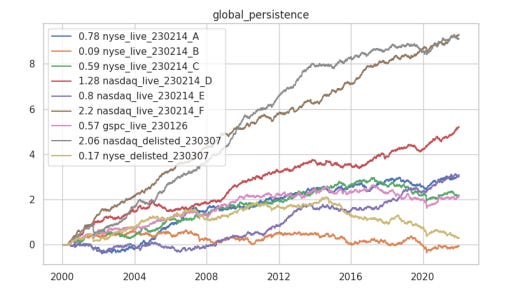
This week we explore a pricing-data based formulaic alpha. The performance results display to us one of the Fundamental Law of Active Management - that the relation between Information Ratio and Number of Trades are related by:

IR = IC * \sqrt{#trades}

In particular, one may expect `quantamental’ strategies to exhibit significantly lower turnover but attendantly lower Sharpe ratios. To see this, refer to the last post’s Signal Migration charts to see that assets change in quantile rankings much more frequently in formulaic alphas based on pricing data rather than fundamental data.

This does not necessarily mean that quantamental alphas are worse, rather that the comparisons drawn between two quantitative alphas need to be adjusted for their level of `activeness’ and cost constraints. Whether they should be included in a multi-strategy portfolio then depends on the fund’s execution ability, other positions in the portfolio and overall manager duration - this should also hint to us that there may be adjustments of trading positions based on active signal decay ~ time distance from signal formation. We shall make it a goal to explore such cost and decay impact models in our future discussions of portfolio management.

Alpha Paper (paid readers):