Implementing a C-level Orderbook in Python
Moving on from our last post on the ringbuffer
This post, we are going to implement a fast limit order book. Examples are taken from quantpylib. Obtain the repo pass here.
Implementation for a Limit Order Book
A limit order book is a data structure representing the market’s supply volumes at various price levels. Dealers in financial markets can post quotes indicating the price they are willing to transact at, and the corresponding quantity of shares they are willing to buy or sell.
A trader can come along and decide to take this liquidity offered by submitting marketable orders that are matched on (typically) price-time priority.
From the quant’s perspective, it is a critical issue to have an accurate mirror of the live order book used by the matching engine. Since this is dynamically changing based on the action of all market participants, the exchange broadcasts updates to client applications.
For instance, a trading application is able to subscribe to these broadcasts through a websocket connection. The messages received are often either snapshot (orderbook state up to some depth) or delta (changes from the previous state) messages.
The problem of the limit order book implementation is to accurately maintain an internal state representation from these messages. A snapshot is often easy to handle, while a delta message typically broadcasts changes as follows:
If price level in delta message exists in local state, take the new volume. If this volume is zero, then throw the price level away.
If price level in delta message does not exist in local state, record this new price level and volume.
If some price level exists in the local state but not the delta message - assume no change.
For a vectorized, numpy implementation:
Except for a number of lines, the code logic is simple to read and understand. Note that we have used the C-level ringbuffer type implemented in the previous post.
Let’s go through the code. The _update method simply implements the delta updates - it combines local states not updated in the delta (new) array and then combines levels with non-zero volume. This is called in update, which does the handling for the different types of messages, and maintains the ringbuffer state.
A slicing/padding is applied when the updated has too many/little levels, respectively. The only peculiar part is the use of shadow_depth.
In general, in order to maintain accurate orderbook state up to level n - we need quite a bit more than n levels. Let n = 3, and initial price 1 through 5. We then receive a price level 4.5, and subsequently cancellation of quotes at 2, 3.
Here are the comparisons with and without additional buffer layers:
[1, 2, 3, 4, 5] +4.5 [1, 2, 3]
[1, 2, 3, 4, 4.5] -2,-3 [1, 2, 3]
[1, 4, 4.5, 0, 0] [1, 0, 0]The above example is self-explanatory. Now that we have implemented the reference behaviour, let's file some complaints.
Let’s ignore the __init__ constructor for a moment - after all, we are most interested in the runtime latency when receiving tick data. Our primary time cost during live trading occurs in the update logic - we can use line-profiler to check which lines are costly:
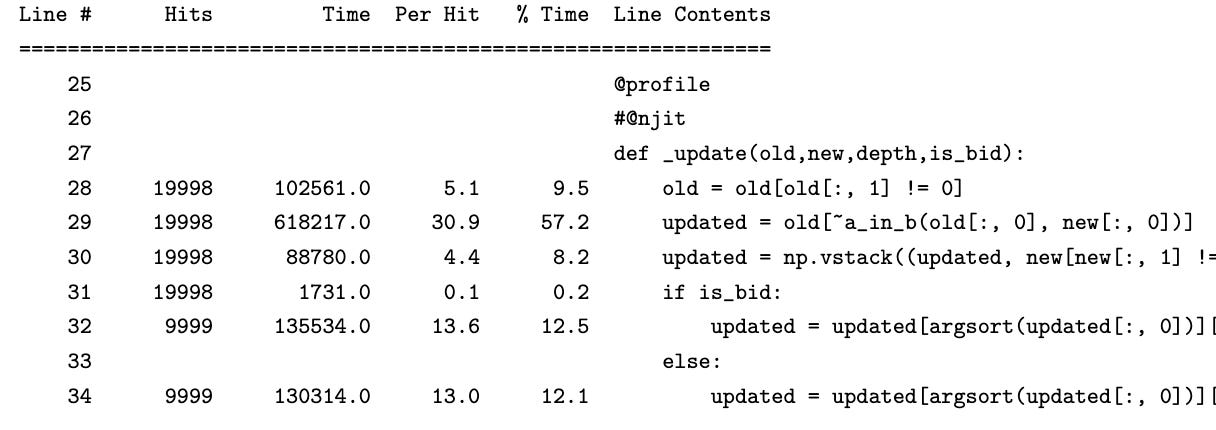
It turns out that 95% of the time is spent in the _update function. Profiling the _update function gives (note that we cannot run the profiler in njit mode)
For each update, even though we are using numba’s runtime (just-in-time) compilation in nopython mode with efficient a_in_b and argsort - we are simply creating too much data! Runtime allocation of memory is expensive. In fact, every single line of code (except the branching and return statement) in _update creates at least one new array.
The good thing is that our Python code leverages numpy’s C-level operations and JIT compilation, offering efficient manipulation. The bad news is that memory allocation, is expensive, period. Shall we do a rough count?
The line old = old[old[:, 1] != 0] creates two new arrays. The line updated = old[~a_in_b(old[:, 0], new[:, 0])] creates three new arrays (one inside a_in_b, another with ~). The line updated = np.vstack((updated, new[new[:, 1] != 0])) creates three new arrays, the boolean mask, the evaluated second argument and the stacked result. Each branch has argsort, which creates new arrays.
If the old array has length m, and new array has length n, then the runtime of the sorting algorithm is O((m + n) log (m + n)). Finally, if there is insufficient depth after the update function, we have to again, allocate more memory to pad depth.
If we can reduce memory allocations, and make use of some guarantees in our data structure, we can do better. The first idea is that since we have already done memory allocation for our current state, we can simply reuse this memory. We achieve this by creating a cache for each side of the orderbook. When we receive new data, we write the correct state to this cache by merging data from our current state array and the new array.
(Section Programming/Python Programming/Cython/Cython in Practice
of our market notes, attached at bottom this post for paid readers)
Continuing…