More on the Black Scholes Digital Pricing
In the previous post, we discussed the need for the digital option pricing model to decompose price uncertainty into diffusion and jump component. The key point was that diffusion plays out and scales risk proportional to the square root of time, while jumps scale linearly. We looked at a possible jump-aware pricing model.
Here we will discuss how this dynamic affects model calibration’s error size and one way to calibrate these parameters. Code is provided. This will be the last post about the subject, because frankly the topic itself was abit of a segue - I would like to continue with the hft notes.
I am also going to do a very interesting series called the Nimble Market Maker - how solo/small quant teams can be competitive in electronic trading.
Okay let’s just get into the mix.
We will first begin by explaining why the jump awareness plays such an important role. Although it is possible in theory to build a volatility surface from more liquid markets, the extreme tte on these market’s suggest that there are very little nearby data points in terms of either strike or term structure; essentially backing out the parameter from a calibrated arbitrage free volatility surface requires extrapolation rather than interpolation, which is much more difficult and error prone from a statistical modelling perspective.
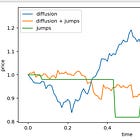
Below is my hand drawn price series, in black there is pure diffusion time-series and in blue, we have a jump-diffusion time series.
The important thing to note is that a derivative that is not jump-aware assumes the total quadratic variation is equal to the integrated volatility of the underlying. In reality, there is jump variation, but from the perspective of the model, there is no distinction between integrated volatility and jump variation.
In model terms, the diffusion/volatility parameter is measured against this quadratic variation. For long-duration assets, this is not particularly important, since the total variation is accounted for by averaging the effect of the jumps over an elevated diffusion metric.
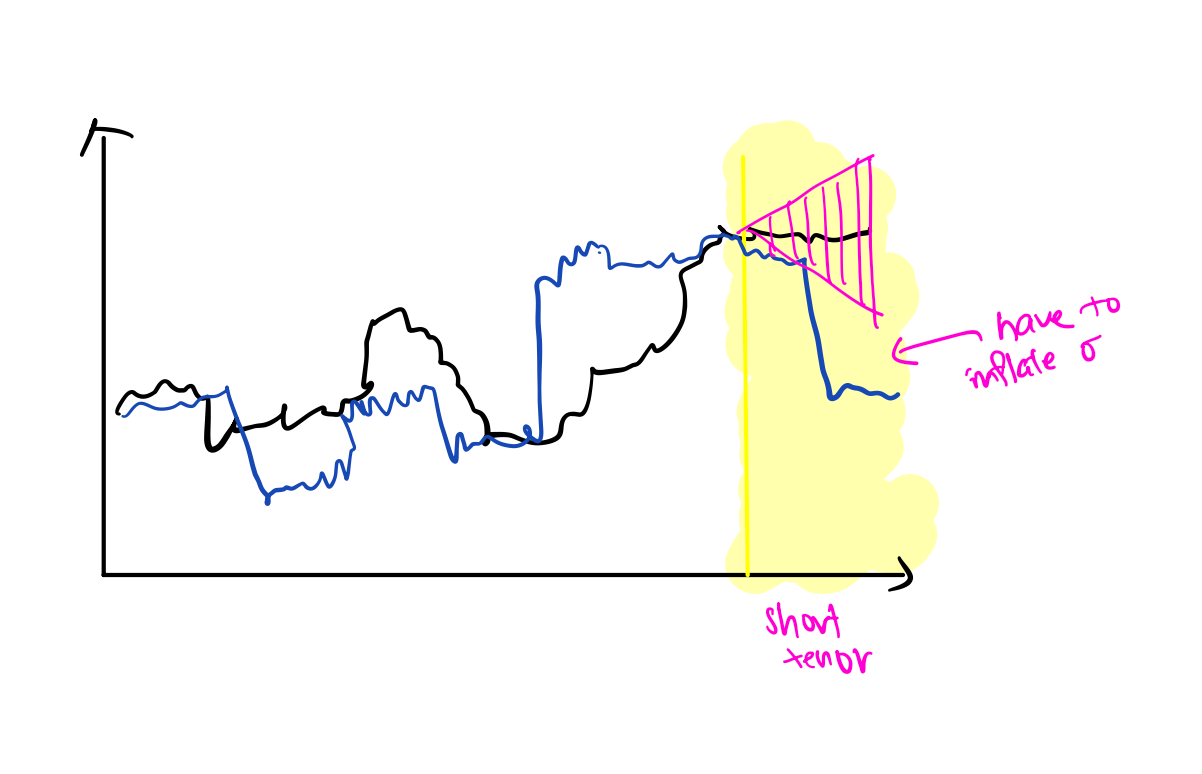
Notice what happens when we approach expiry (shaded yellow). When the price can incur jumps, traders are much more willing to accept the possibility that the underlying will be significantly different even in a short time span. The number of such jumps is typically modelled as a Poisson random variable. In the jump-unaware case, in a short amount of time, diffusion can only effect price changes through returns up to the statistical artefacts of a Gaussian distribution, a ‘cone’ shown in pink.