On the OMS hedge order
In the last post:
we demonstrated our quantpylib.hft.oms module, and showcased some complex orders. Since then, we’ve made some meaningful improvements, including the self-error correcting mechanisms in the OMS to account for disconnects in the socket subscriptions. We will talk about these in the next post.
For now, I want to talk more about the hedge order, which some readers have reached out to me about. I will describe how it is implemented.
Please read the previous post on how it is called. Otherwise, this post may not make much sense.
Recall that the one of the roles of the OMS is to standardize exchange message schema - so that order information is recorded in a standardized way - regardless of the exchange traded. This representation allows our trading agent to implement algorithms relative to the business logic defined internally.
From the previous post, each order update message from the exchange is first parsed into standard schema. Since we already maintain an internal state of the orders page, regardless of the message received, we can push out an `orders delta/change` message by comparing the new order information to stored order information.
Recall that users of the OMS can register an arbitrary number of handlers that receive the broadcast order delta messages asynchronously. This architecture allows us to register any number of default handlers on OMS initialization, that allows us to support any complex order type including custom TWAP/VWAP logic and so on, should we implement it down the line.
Immediately after the OMS is created, we register a default handler:
called order_delta_hedge - this is the hedging algorithm and handler that receives order delta broadcasts. Since we need to track hedge orders called by the user, at object initialization - we keep a reference to the client order ids -
see that we have self.hedge_book and self.hedge_balance. This is a mapping for exchange > ticker > hedge information.
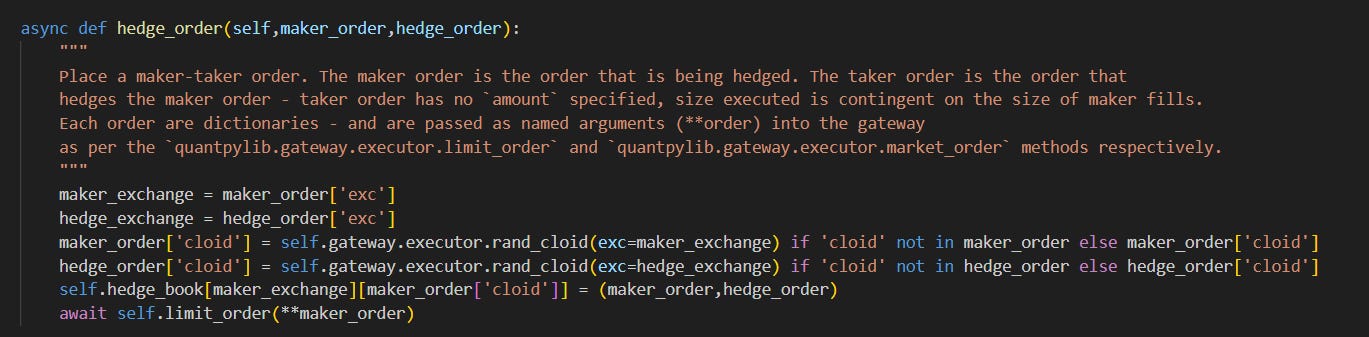
When a hedge order is called:
The maker’s client order id is stored in the hedge `book` . The hedging order is stored alongside it, with the order configurations. When this maker order is partially or fully filled:
we use the client order ID to retrieve the hedge order, infer the filled size of the order and use this to hedge. If there is an existing balance that is unhedged (due to previous rounding errors in cross-exchange contract rules), we group them together and hedge as much as possible - while storing the remaining back in the hedge balance. A tiny detail is the use of floor_to_n in the n^th precision - since often partial order fills often arrive sequentially and instantaneously. We don’t want to round-up, otherwise the next fill received may be an `overflow`.
From a learning POV, while this seems like a fairly non-trivial result - a number of important decisions in the software dev process allows us to arrive at this result. For the purpose of learning, I will reiterate them.
For us to achieve complex orders, a standardized schema for business objects are required - that is, things like account margins, balances, orders, positions, trades, order book - all should have internal and separate representations.
This goes the same for business logic - things like generating client order IDs, internal order configs > exchange order configs.
It is only when 1+2 is sufficiently abstracted that auxiliary layers (such as the hft.OMS and hft.Feed) can be written on top of the gateway logic.
Hopefully these posts are helpful for beginner devs in making engineering choices in their own quant systems and bring you one step closer to `in-house` architectures.
Of course, it is a work in progress…
I keep developing in the quantpylib repo, and more will come. Quantpylib is a repo for annual subscribers:
cheerios!